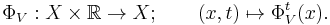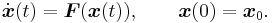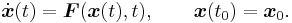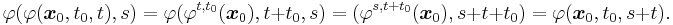Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over time. More formally, a flow is a group action of the real numbers on a set.
The idea of a vector flow, that is, the flow determined by a vector field, occurs in the areas of differential topology, Riemannian geometry and Lie groups. Specific examples of vector flows include the geodesic flow, the Hamiltonian flow, the Ricci flow, the mean curvature flow, and the Anosov flow.
Contents |
Formal definition
A flow on a set X is a group action of the additive group of real numbers on X. More explicitly, a flow is a mapping
such that, for all 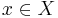 and all real numbers s and t:
and all real numbers s and t:
It is customary to write φt(x) instead of φ(x, t), so that the equations above can be expressed as φ0 = id and φs ∘ φt = φs+t. Then for all t ∈ R the mapping φt: X → X is a bijection with inverse φ−t: X → X. This follows from the above definition, and the real parameter t may be taken as a generalized functional power, as in function iteration.
Flows are usually required to be compatible with structures furnished on the set X. In particular, if X is equipped with a topology, then φ is usually required to be continuous. If X is equipped with a differentiable structure, then φ is usually required to be differentiable. In these cases the flow forms a one parameter subgroup of homeomorphisms and diffeomorphisms, respectively.
In certain situations one might also consider local flows, which are defined only in some subset
called the flow domain of φ. This is often the case with the flows of vector fields.
Alternative notations
It is very common in many fields, including engineering, physics and the study of differential equations, to use a notation that makes the flow implicit. Thus, x(t) is written for φt(x), and one might say that the "variable x depends on the time t". Examples are given below.
In the case of a flow of a vector field V on a smooth manifold X, the flow is often denoted in such a way that its generator is made explicit. For example,
Orbits
Given x in X, the set 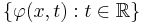 is called the orbit of x under
is called the orbit of x under 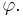 Informally, it may be regarded as the trajectory of a particle that was initially positioned at x. If the flow is generated by a vector field, then its orbits are the images of its integral curves.
Informally, it may be regarded as the trajectory of a particle that was initially positioned at x. If the flow is generated by a vector field, then its orbits are the images of its integral curves.
Examples
Autonomous systems of ordinary differential equations
Let F:Rn→Rn be a (time-independent) vector field and x:R→Rn the solution of the initial value problem
Then φ(x0,t)=x(t) is the flow of the vector field F. It is a well-defined local flow provided that the vector field F:Rn→Rn is Lipschitz-continuous. Then φ:Rn×R→Rn is also Lipschitz-continuous wherever defined. In general it may be hard to show that the flow φ is globally defined, but one simple criterion is that the vector field F is compactly supported.
Time-dependent ordinary differential equations
In the case of time-dependent vector fields F:Rn×R→Rn one denotes φt,t0(x0)=x(t), where x:R→Rn is the solution of
Then φt,t0(x_0,t,t0) is the time-dependent flow of F. It is not a "flow" by the definition above, but it can easily be seen as one by rearranging its arguments. Namely, the mapping
indeed satisfies the group law for the last variable:
One can see time-dependent flows of vector fields as special cases of time-independent ones by the following trick. Define
Then y(t) is the solution of the "time-independent" initial value problem
if and only if x(t) is the solution of the original time-dependent initial value problem. Furthermore, then the mapping φ is exactly the flow of the "time-independent" vector field G.
Flows of vector fields on manifolds
The flows of time-independent and time-dependent vector fields are defined on smooth manifolds exactly as they are defined on the Euclidean space Rn and their local behavior is the same. However, the global topological structure of a smooth manifold is strongly manifested in what kind of global vector fields it can support, and flows of vector fields on smooth manifolds are indeed an important tool in differential topology. Also a bulk of study in dynamical systems is conducted on smooth manifolds, which are thought of as "parameter spaces" is applications.
Solutions of heat equations
Solutions of wave equations
See Also
References
- D.V. Anosov (2001), "Continuous flow", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=c/c025630
- D.V. Anosov (2001), "Measureable flow", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=m/m063190
- D.V. Anosov (2001), "Special flow", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=S/s086270
- This article incorporates material from Flow on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
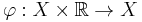
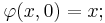
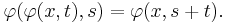
![\operatorname{dom}(\varphi) = \{ (x,t) \ | \ t\in]a_x,b_x[, \ a_x<0<b_x, \ x\in X \} \subset X\times\mathbb R](/2012-wikipedia_en_all_nopic_01_2012/I/bddfc41c90418a89a66f7ff455cbe341.png)